Più simile a una formula magica che a una legge matematica la Legge di Benford è usata per la rilevazione di frodi e di falsi e per individuare la genuinità di distribuzioni casuali di numeri. Descrizione, esempi di applicazione ed esperimento su questa legge.
Descrizione
Sono venuto a conoscenza dell’esistenza di questa legge vedendo una puntata di Connected, una serie di documentari di Latif Nasser su Netflix.
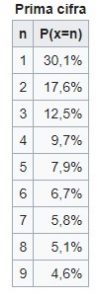
Secondo questa legge, se si prende una raccolta di dati reali e si analizzano i numeri che la compongono prendendo in considerazione solo la prima cifra significativa di questi numeri (per esempio: 1.2 diventa 1, 3678 diventa 3, 0.8 diventa 8) allora si può verificare che il numero di occorrenze di ciascuna cifra rispetta una proporzione ben determinata.
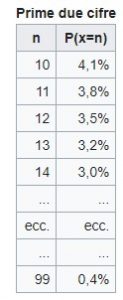
Ovvero: I numeri che cominciano con “1” sono il 30,01%, i numeri che cominciano con “2” sono il 17,6% e così via:
|
|
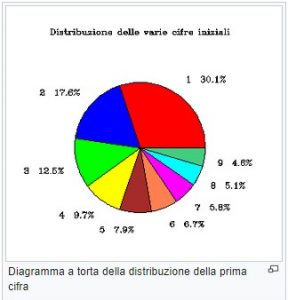 |
In modo più formale la Legge di Benford può essere definità in questo modo:
![]()
Dove P(n) è la frequenza con cui deve essere presente la cifra n.
Esempi d’utilizzo
I dati da analizzare possono essere di qualsiasi tipo, possono riguardare le cose più disparate e possono essere estratti:
- da una dichiarazione dei redditi,
- da un bilancio di una azienda o di uno stato,
- dalla codifica di una immagine digitale,
- dai risultati di una elezione,
- dalla sequenza del fatoriale di un numero,
- dal risultato di un censimento o di una indagine statistica,
- da dati astronomici (es. distanza di pianeti o stelle dalla Terra)
e così via.
Ma cosa c’entra tutto ciò con la scopera delle frodi e perché questa legge viene usata dalle Agenzie Fiscali di tutti i paesi per scoprire i bilanci falsificati?
In pratica se una sequenza di numeri non ha una “origine reale” e quindi casuale, ma è stata manomessa per ottenere un preciso scopo (es. per pagare meno tasse) allora non rispetta più la legge di Benford.
Detto in altri termini, se si prende una sequenza di numeri e questa sequenza non rispetta la Legge di Benford, allora è quasi sicuro che questi numeri sono stati manomessi e non sono “genuini”.
E’ per questo che questa legge viene usata per verificare la bontà dei dati nei campi più disparati. Sul sito Testingbenfordslaw.com [4] o nella puntata 4 (Cifre) del documentario Connected [8] è possibile vedere alcuni esempi di utilizzo della legge.
Quindi il grafico di una sequenza “genuina” è:
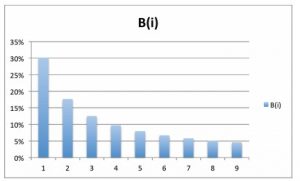
Il grafico della frequenza di una sequenza “manomessa” potrebbe essere di questo tipo:
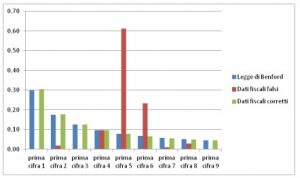
I dati in rosso sono quelli falsificati, quelli in verde quelli originali.
Spiegazione della legge presente sul canale Youtube dell’Università Bicocca di Milano:
Esperimento
Ho provato ad applicare questa legge ai dati pubblicati dall’OMS riguardo alla diffusione del Corona Virus [7].
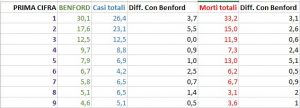
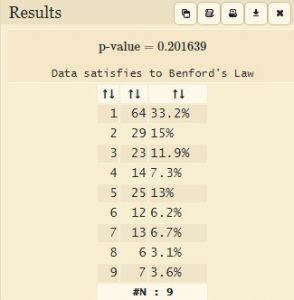 |
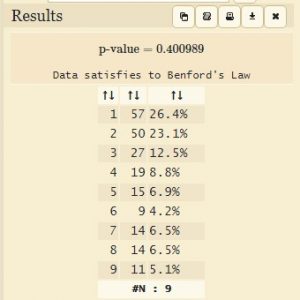 |
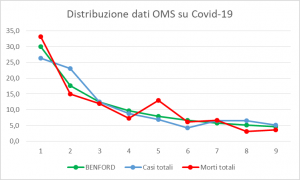
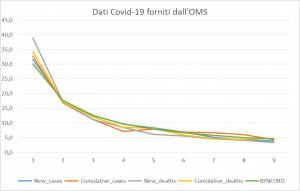
Condisiderazioni
Non sono a conoscenza di una dimostrazione di questa legge, la cui validità è però empiricamente verificabile.
Fonti e riferimenti:
- Legge di Benford su Wikipedia.
- Video sulla legge di Benford dell’Università Bicocca di Milano.
- Tool online per verificare la legge su raccolte di numeri.
- Alcuni esempi online della legge.
- La legge di Benford: imparare a intercettare le frodi di Christiane Rousseau.
- La legge di Benford, Appunti dell’Università Bicocca di Milano.
- Dati ufficiali sul Covid-19 dell’OMS (Organizzazione Mondiale della Sanità, WHO).
- Connected su Netflix (Stagione 1 – Puntata 4 – Cifre).
- Analisi dei dati e prevenzione delle frodi con la Legge di Benford (Applicazione di Benford a un caso reale) di Gaetano di Marco su Geotrading.it.
- Definizione del Valore p (p-value) su Wikipedia.